拉格朗日计划数问题来源于拉格朗日的四平方和定理,该定理断言:任何自然数都可以表示为最多四个整数的平方和。这一数学定理不但在理论数学中有着重要的地位,也给现代手游设计提供了无限的灵感。游戏设计师们利用这一数学问题设计了许多富有挑战性且引人入胜的游戏关卡和谜题,玩家需要通过逻辑思维和策略规划来解决问题,从而通关。
在手游中,拉格朗日计划数问题主要以谜题和挑战的形式出现。设计师们通过设置不同的游戏情景和规则,使玩家在尽可能少的步骤内找出特定数值的平方和,以解锁新的游戏关卡或获取特殊奖励。这种类型的游戏不仅锻炼了玩家的思维能力,也极大地提升了游戏的趣味性和挑战性。
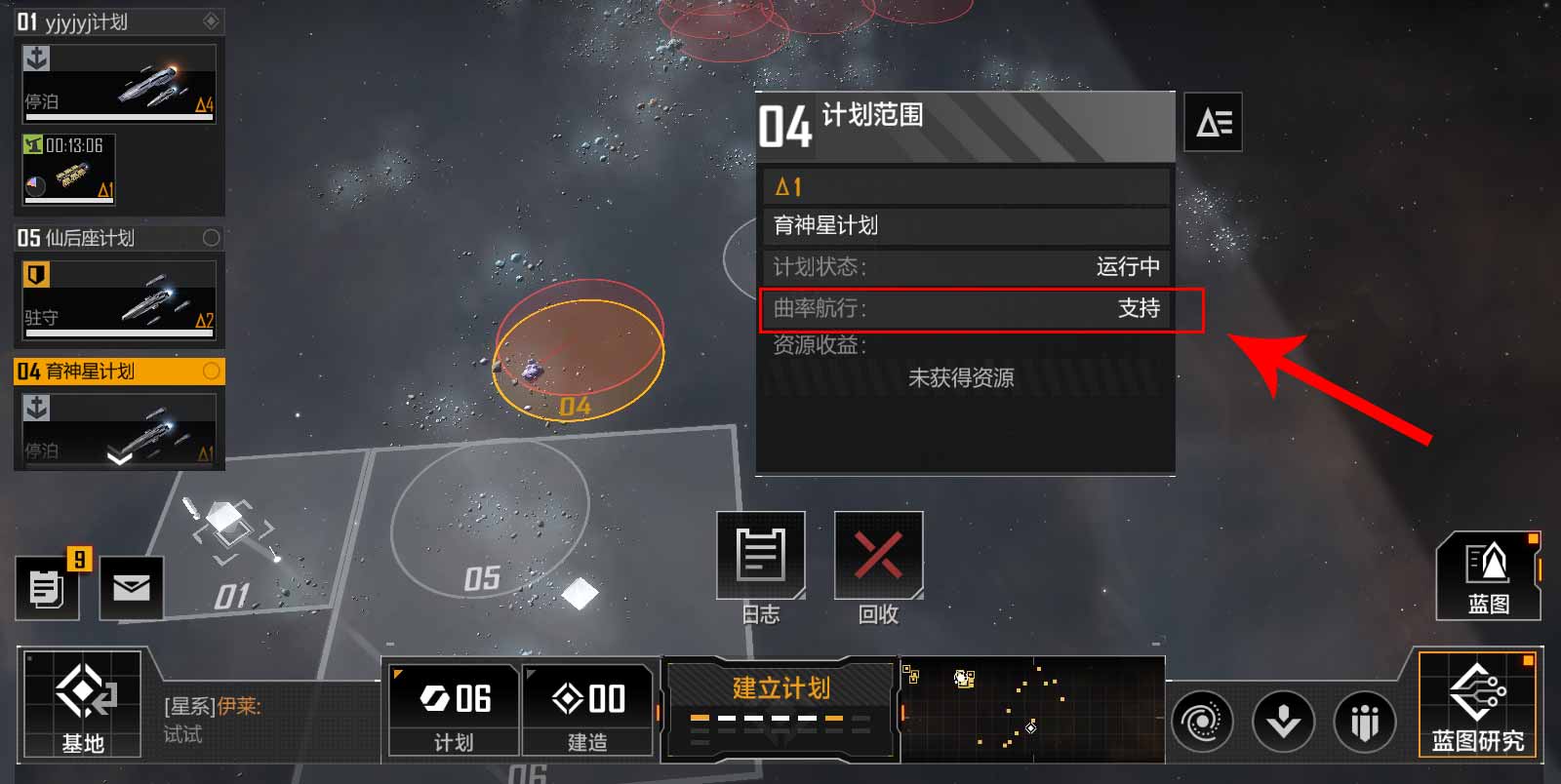
理解数学原理:玩家需要对拉格朗日四平方和定理有基本的理解和认识,这有助于在面对游戏中的数学问题时能够快速找到解题的思路。
逐步分解法:在游戏中遇到复杂的数值时,可以尝试将其分解成更小的数值,逐步分解并找出各个小数值的平方和,最终组合成最终答案。
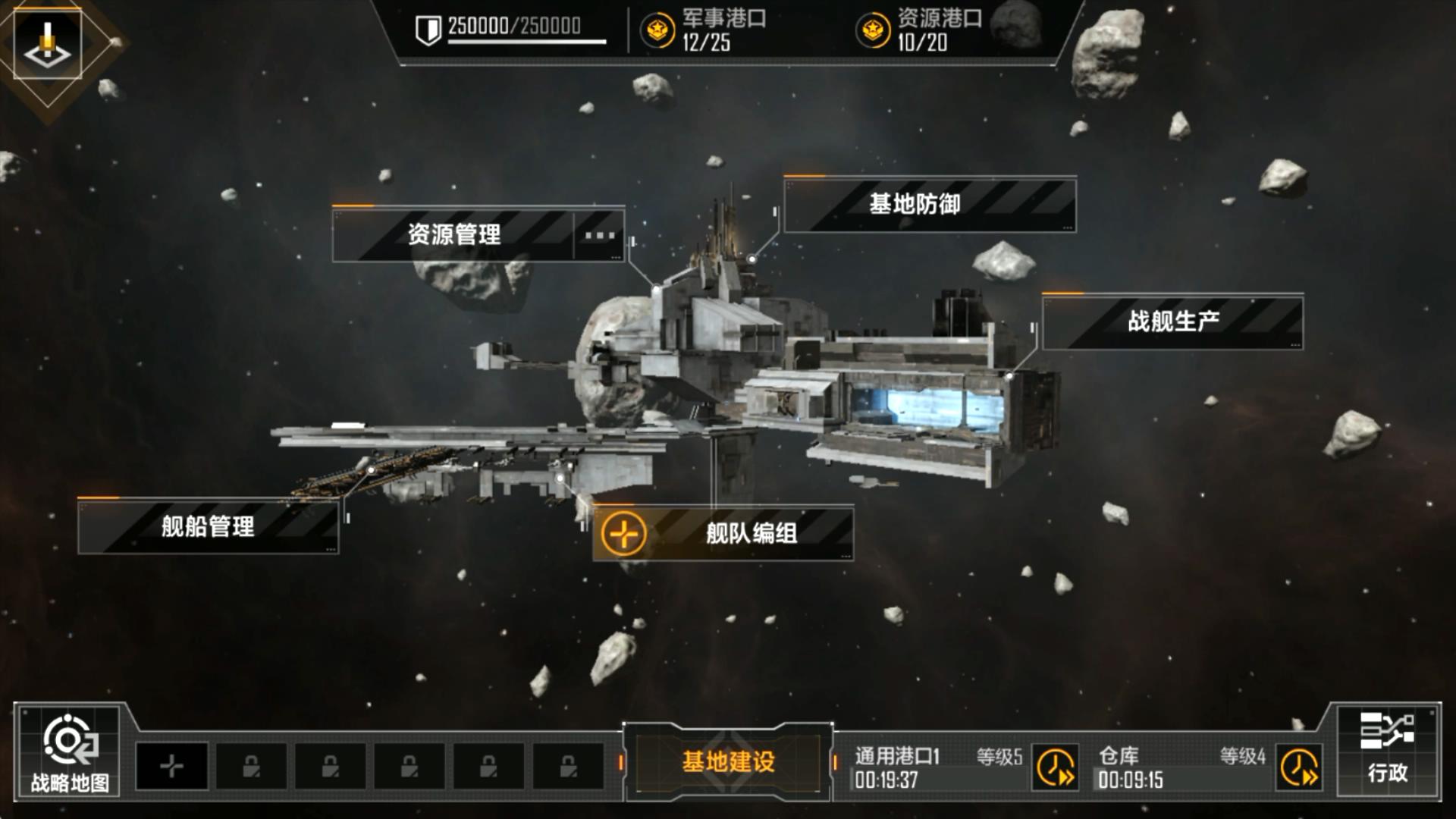
利用软件工具:有些游戏允许玩家使用外部软件工具。通过软件工具的辅助,如在线拉格朗日计划数计算器,玩家可以更快速地找到数值的平方和。
交流与合作:有的游戏设计了团队模式或社区交流平台,玩家可以互相交流想法和解题技巧,借助他人的智慧来解锁难题。
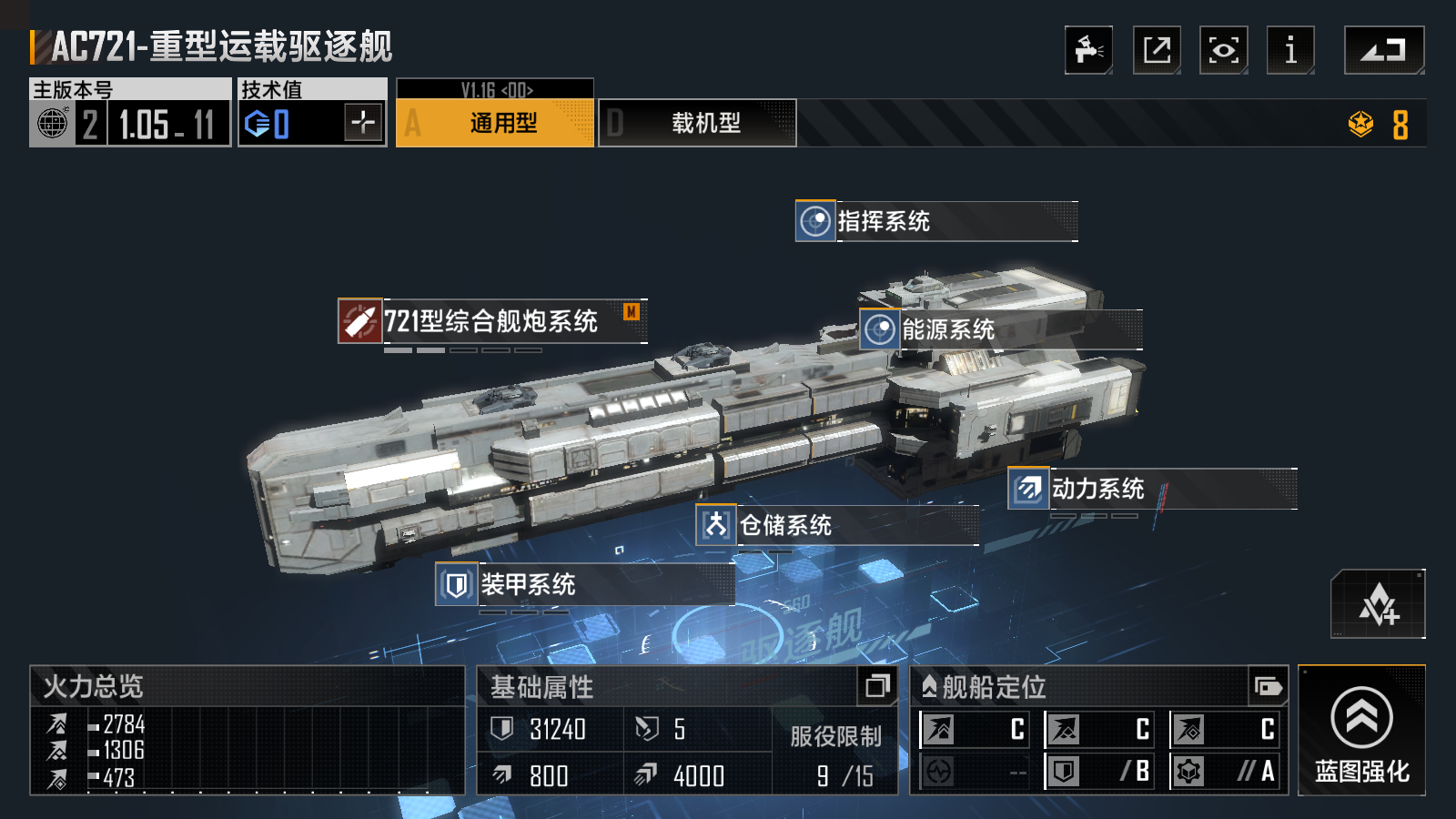
玩家体验:通过设计策略解除无尽的拉格朗日计划数问题,可以极大地提升玩家的游戏体验。挑战性与趣味性的结合让玩家在享受游戏的同时锻炼了自己的数学思维能力。
游戏设计发展:探索和实施解除无尽的拉格朗日问题的策略,促进了游戏设计的创新和多样性。游戏开发者在解决这一数学问题的过程中获得了宝贵的经验,这些经验可用于未来更多更复杂游戏的设计之中。
教育价值:手游中解决拉格朗日计划数问题的过程,实际上也是一种寓教于乐的方式。许多教师和家长开始意识到,这类游戏可以作为数学教学的辅助工具,帮助学生在轻松愉快的环境中提高数学和逻辑能力。
综上所述,手游中的拉格朗日计划数问题不仅为玩家带来了无尽的挑战和乐趣,同时也促进了游戏设计的创新和教育领域的发展。通过逐步分解、利用软件工具、以及团队合作等策略,是有可能解除这一数学难题的。随着科技的不断进步和游戏设计理念的不断发展,我们有理由相信,将会有更多创新和有趣的方式被开发出来,以解开手游中无尽的拉格朗日计划数问题。